The Power of Probabilistic Thinking
Even Brilliant People Can Be Wrong
In my book, very early, I explain to the reader that my goal is not to teach them WHAT to think, but HOW.
Notoriously, I asserted “The Polls Weren't Wrong” regarding Trump 2016, Brexit, and a few other highly contentious elections. That assertion (the WHAT) was based on a detailed presentation of reasoning and findings (the HOW). While the conclusion is certainly the “headline” - it is secondary to the book’s more consequential discoveries:
Experts literally don't understand what polls are supposed to measure.
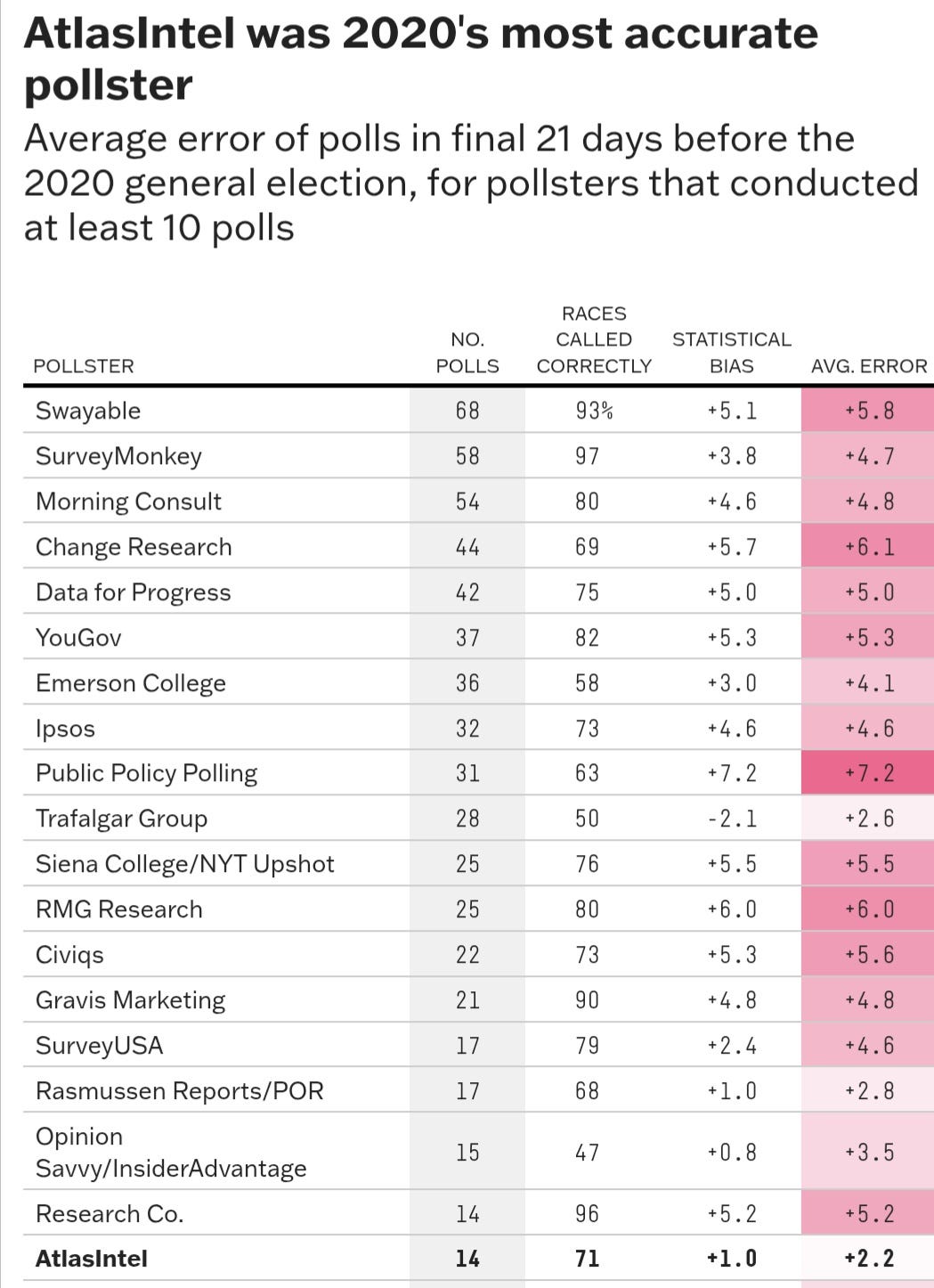
, , and panels of analysts around the world - in their own words and calculations - prove it.Different countries measure poll accuracy using different, contradictory methods based solely in tradition, not scientific rigor.
Otherwise reputable pollsters are being demeaned and forced out solely due to unscientific standards.
I strongly encourage (and challenge) any analyst or researcher to contend my findings, because that's how science works. But they won't, because they can't.
My process is scientific, theirs is not. My conclusions follow logically, theirs do not - that's all there is to it.
Even if, somehow, my conclusion is wrong (i.e. the flawed methods used in calculating poll accuracy did not contribute a substantial amount to the claimed “error” in Brexit, Trump 2016) - that does absolutely nothing to address the indisputable problematic facts bulleted above - among others not shown!
Here's why:
The collection of people who analyze political polls - and educate the media and public on the topic - are surprisingly uninformed of scientific validity.
It goes back to how you think about complex problems, and how (and if) you quantify uncertainty.
Deterministic Reasoning: Assumes an event follows a cause-effect relationship - that given enough data, the outcome can be known in advance.
Probabilistic Reasoning: Acknowledges that (some) events are inherently unpredictable or contain some amount of uncertainty: there is no amount of data that would allow us to know the outcome in advance.
In my mind, for many years, I viewed Deterministic Reasoning as “lazy” and Probabilistic Reasoning as “rigorous.”
But that's not quite right. Experts in psychology would argue it's not right at all. And…they might be right.
To my surprise, these two forms of reasoning literally use different parts of the brain.
Deterministic thinking, which seeks binary truths and clear outcomes, tends to activate rule-based, logical networks - especially in the frontal and parietal regions.
Probabilistic thinking, on the other hand, draws heavily on memory systems and pattern inference, especially in the hippocampus, where past experiences and uncertainty are evaluated.
In other words, your brain literally switches gears when shifting from one form of reasoning to the other!
So it’s not a matter of “lazy” versus “astute.” That’s a misdiagnosis. It's a question of understanding which form of reasoning is best applied to the situation.
If you’re checking a mathematical proof, diagnosing a mechanical failure, or evaluating a chain of logic, deterministic reasoning is exactly the right tool. It’s clean, efficient, and powerful.
For a simpler example, if someone says “I'm holding a bowling ball above my head, what will happen if I drop it?”
It doesn't make sense to theorize about the probability that the laws of nature will be suspended in the next few seconds. Here, Probabilistic Thinking doesn't serve a purpose, it would only complicate what is a very simple answer: it will fall.
Here, the evolution of the human mind is on full display: an approximately correct, quick answer is far preferable to a perfectly accurate but slow one.
Our brains weren’t shaped to win logic prizes, or make probabilistic calculations at all. They were shaped to avoid getting killed. If you hear a strange rustle in the bushes, your brain doesn’t pause to calculate a 2% chance of predator, 48% chance of wind, and 50% chance of small mammal. It just screams:
“sh*t, f**k, something wants to kill me, run away.”
Indeed, this evolutionary anxiety is something most have experienced in their own home.
If you hear a loud crash of broken glass in the other room, your brain probably doesn't tell your body, “something probably just fell, it's not a big deal.”
The brain flips what is best quantified as probabilistic input into a binary response, instantly: danger. Protect yourself.
In science class, you learn about false positives and false negatives, and it's a fine lesson. But our survival instincts are hard-wired, and even if we've experienced 99 loud, weird noises in our home that were harmless, we're still going to be hypervigilant the 100th time.
This doesn’t mean our inclination towards deterministic reasoning is irrational, it means we’re built for survival, not statistics.
Overcoming your brain’s natural wiring - but only when you choose to - requires some training and practice.
Train Your Brain - Easy
I have a fair coin. I will flip it. I want to know:
Will the next flip be heads?
Even though the next flip will be, with 100% certainty, heads or tails, there is no amount of data that would allow someone to answer “yes” or “no.”
As you know, the correct answer is a probability. In this case, the “correct” probability can be known: 50-50.
So, will the next coin flip be heads?
The best answer: “There's a 50% chance.”
Even with an improperly framed question, probabilistic thinkers can still stay consistent.
In this case, that's the only right answer. The actual outcome, whether heads or tails, doesn't impact the “correctness” of my forecast.
Most of you, I'm guessing, got that easily. I believe that's for two reasons:
You know the correct probability calculation
You do not have an emotional connection to the outcome
Foreshadowing, the same cannot be said for election results.
Competing Coin Flip Forecasts - Who Is Right?
Assume there are two competing Coin Flip forecasters. They both have access to the following data:
The last 9 coin flips have totalled 4 heads, and 5 tails. The most recent coin flip was tails. There will be one more coin flip.
Carl's forecast: coin flips are independent. There's a 50% chance the next flip is heads.
Competitor's forecast: in the long run, flips will be 50-50, so with the last flip being tails and tails being up 5-4 gives a higher probability of heads. 67% chance of heads.
Result: the coin flip is heads.
Who was right? Whose forecast was better?
My competitor assigned a higher probability to the eventual outcome.
Given this example, you might think it's foolish to say that simply assigning a higher probability to the eventual outcome in itself makes a forecast better.
And yet applying that simple knowledge to real-world examples would make you elite as it pertains to statistical analysis.
My approach to analyzing political forecasts does nothing more than take this simple example and apply it to a more complex one:
The probability, without an enormous sample size - because it's impossible in political circumstances - cannot be “long-runned.” We must rely on underlying logic, and scientific validity.
For that reason, “who is right?” or “who is better?” is not quite as simple as it appears.
Most people think this is an example of overcoming the Deterministic temptation. I've often heard it cited as such. They believe this example illustrates they understand that a forecast that assigns a higher probability to the eventual outcome is not necessarily better. Without “training” some do, maybe, but very few.
Most don’t. Here's why:
In the coin flip example, you know the right probability to assign.
In this case, you're not viewing the result and then retrospectively judging the forecast accuracy. You know, from both math and experience, that a fair coin lands heads 50% of the time. That makes it straightforward to show why the 50% forecast is correct and the 67% forecast is overconfident. You understand (at least, in this specific application) the result is irrelevant to what the best forecast is or was!
Notice: this is deterministic reasoning! You have a known “true” probability (50%), and you’re measuring each forecast against that single, fixed benchmark. It’s easy to evaluate the quality of the forecasts because there’s no ambiguity about what the correct answer is.
And in this case, deterministic reasoning is exactly what you want! There’s no need for nuanced probabilistic judgment when the right answer is known and provable.
In this example, you don't have to spend time wondering about the possibility that my competitor’s forecast incorporated some hidden or advanced knowledge about the result of the next coin flip.
Herein lies the first lesson:
Deterministic reasoning is not always a bad thing. Sometimes it’s more than acceptable, it's best.
When forecasting an uncertain future event, it requires assigning a probability. The best answer is the one that is closest to the true probability* - the outcome of that event is irrelevant!
*There is more nuance than this, but for “basic” it will suffice.
More foreshadowing: when the “true probability” is unknown, our brain does that thing where we (consciously or subconsciously) believe the actual outcome must have been the most likely one - whether that's true or not. This incorporates a few different forms of fallacious reasoning, the most prominent of which is hindsight bias.
I can prove it with what I have coined to be the “textbook” example for political poll data measurements:
Train Your Brain - Medium: Which Poll is More Accurate?
Consider two competing polls in a two-way election.
Poll 1:
Candidate A: 46%
Candidate B: 44%
(10% undecided)
Poll 2:
Candidate A: 44%
Candidate B: 46%
(10% undecided)
Election Result:
Candidate A: 51%
Candidate B: 49%
Which poll was more accurate?
The current standards, in addition to most everyone when presented with this problem, would agree: Poll 1 was more accurate.
The field's (un)scientific consensus is not only that Poll 1 was more accurate, but it also had a 0 point error!
The calculation is that Candidate A was up by 2 in poll, and won election by 2.
Meanwhile, Poll 2 had a 4 point error (Candidate A down by 2 in poll, but won by 2).
There is one right answer to this question. The consensus, undisputed, universally accepted answer is that Poll 1 was more accurate.
The consensus literally says, and believes “polls predicted…” is valid logic, and a valid calculation.
This is not the right answer!
Yes, it is that simple.
Let me be VERY clear:
This is a math problem, or a probability problem to be more precise. If your answer to a math problem is wrong, I prove it wrong, and your response is to complain about my writing style, boast about your experience or degrees, then you have admitted that you are not qualified to debate the subject. It's nothing personal, that's just how science works.
Suitably, there's very recent precedent for experts being wrong about a math problem, and getting proven wrong by a relative outsider to the field. It happens.
And in this political polling problem, the field's experts have mistakenly accepted that the result is the correct answer for poll accuracy. Not just any result, but the “margin of victory” in the result.
To be nice (or mean, depending on how you take it) - they're using the wrong part of their brains for this problem. Not lazy, not dumb, just mistaken.
I'll be succinct: polls are probabilistic tools, not deterministic ones. Indisputable. While it's plenty appropriate to judge a tool's accuracy by its closeness to the “true value” - you have to use the correct true value! You can't judge a probabilistic tool’s accuracy by how well it predicts a specific future result.
For example, if you believed the result of the coin flip was the true value, you'd be perfectly content saying the forecast with the higher probability was more accurate.
Indeed, that is literally how poll accuracy is currently judged - by how well it predicts the result. That is not my interpretation, that's a direct quote!
The right answer to the “medium” Train Your Brain question is given in this article.
A “medium” question to ask yourself is:
“Is it possible that Poll 2 was more accurate than Poll 1? How likely is it?”
This is probabilistic reasoning. The right answer requires assigning probabilities.
There is no way to know with certainty which poll(s) were most accurate in any given election - a fact that is directly contradicted by every major organization who grades polls and poll averages on this basis.
I've already solved these problems, and more, while no one else in the field has even thought to ask the questions yet!
“Here are the polls. Based on this result, which polls were more accurate?” Is a nonsensical question. No one who understands how polls work would ask it, or try to solve it - yet everyone does.
There is far too much important data missing and unaccounted for in this calculation. It's embarrassing that anyone would try to pass this as analysis, frankly. Yet
does, and did, every election: and he's one of the better analysts!By the way, even if you had data with ZERO margin of error, you still can't answer the question of “which is better?” (which I also proved here and here).
As you may understand - even if the experts in the field don't: polls and forecasts are different things.
The number of messages I've received from intelligent people (up to and including bonafide academics) asking me about “what went wrong” with my Presidential Forecast model in 2024 - for assigning Kamala Harris a 67% chance of victory in an eventual loss - is indicative of this misapplied reasoning.
To be clear, this is not to say my model couldn't have been flawed. If you want to dig into the interstate (or intrastate) covariance, or any number of other variables that could cause my model to have produced a poor probability - fine.
But because election forecasting is such an emotional topic, our brains don't use the “slow, rational” part. It uses the “fight or flight” part.
Loud crash? Definitely danger. Run away.
Your forecast said they were favored then they lost. Bad forecast.
Same process.
Textbook Hypocrisy
When Nate Silver rose to fame on the back of a 2008 and 2012 election, this is how it was reported:
“Silver predicted not only Barack Obama's victory but the outcome of the presidential contest in all 50 states.”
No one, that I'm aware of, wrote any letters to the editor or bothered to correct them - and this is indeed a line regurgitated by academics and media alike. It's common, and problematic.
Silver provided probabilities that Obama would win those states, and he provided a probability that Obama would win the election. The fact that the model was flawed is beside the point: the much more pertinent problem is interpreting probabilities as “calls” or “predictions.”
It's easy to accept undue credit when it makes you look good. But it's poor science. And in 2016, when Silver said Clinton was favored (and she lost) - suddenly, everyone else is stupid for not understanding probability.
You don't get it both ways.
If you don't correct people for saying you “called it” when the outcome you think is most probable happens, you have no credibility to do so when it doesn't.
The challenge - and why this level of thinking is harder then it seems - is that the “true” probability that someone would win an election, unlike coin flips, is not known or knowable. It can never be known.
The coin flip example has randomness built into the system: it has aleatory uncertainty. But because we know all of the relevant variables, we can precisely quantify it.
The election example has too many variables (and confounders) to quantify precisely, and the system is too complex to test or backtest a “correct” probability: this is epistemic uncertain.
Because of this discomforting truth of “epistemic uncertainty,” (don't know, can't know) plus the fact that we have strong emotional connections to election outcomes, our brain rationalizes what we observe - the result - with the expectations we had prior.
Obama won in 2012, so we retroactively assign a 100% probability to that outcome. Those closest to that are declared “best.”
Repeat for Trump 2016. He won, therefore anyone who said he was an underdog must have been wrong.
It's this misapplication of deterministic reasoning that draw people to hacks like Christopher Bouzy and Alan Lichtman who both confidently make declarations based on non-existent models (Bouzy) and pseudoscientific “keys” (Lichtman).
Indeed, someone within my network who has a lot more power in this country than myself asked a few years ago for:
“Someone who predicted Trump would win, COVID would kill a lot of people, and that Bitcoin would become very valuable.”
The thought process being: anyone who predicted all these things must be very good at predicting things.
But the reality is that all of those events, before they happened, were only a probability. Anyone who claims to have “predicted” them is - in a bitter twist of irony - unqualified to do any job my friend would want.
Want to talk about the probabilities that they would happen, the assumptions of the models that produced those probabilities, or how this is just the hot hand fallacy repackaged to world events?
Of course not. You just want to know who knew.
We misuse deterministic reasoning like “right” and “wrong” because of this hindsight bias: we assume events that could not have been known in advance, maybe, could have been. We find things that, if only we had incorporated this information, we would have been right.
(This exact reasoning has been used to declare online polls are better, weighting by education is absolutely necessary, and many other things…based on hindsight.)
When we don't know how things work, we seek people who do - or claim to - to give us the answer.
The answer in political forecasting is: there is no answer. It's all a probability. Anyone who tells you they “know” or “knew” is lying to you. Without exception.
Are there ways, then, to determine whose forecasts are better, if not just the result?
Definitely.
But that's apparently too advanced for the field right now.
I hope to fix that - or put us on the path to fixing it.
Train Your Brain - Advanced
If you found this article insightful, interesting, or just plain easy, I strongly recommend that you buy my book.