The Monty Hall Problem: On The Shoulders of Giants

Featuring: Mean Ol' Marilyn

One of the most famous probability problems, only recently solved, illustrates how ill-equipped a field's experts can be when presented with subtle variable change and an unintuitive answer.

You may be aware of the solution, but you may not know that this problem was the center of heavy debate, and offers a very recent example of otherwise smart people being disproven about a basic statistical concept.

Perhaps made more famous by its presence in the movie “21", professor and card-counting ringleader presents the problem to a new student, who solves it remarkably quickly, on the spot, in front of the whole class.

In case you've been living behind a door, here is the problem:

Suppose you're on a game show, and you're given the choice of three doors. Behind one door is a car; behind the others, goats. You pick a door — say, No. 1 — and the host, who knows what's behind the doors, opens another door, say No. 3, revealing a goat. He says to you, "Do you want to switch to door No. 2?" Is it to your advantage to switch your choice?

The Background

Known as the Monty Hall Problem, after the host of “Let's Make a Deal” where the game was played, I'd wager most readers of my work are familiar, and may even know the answer.

But I want to show some rare humility here, and perhaps inspire some. To use an example outside the field of statistics, I'll say I was a passable calculus student. But if I were given the same lessons and equations in 1800 instead of 2000 - Newton’s notation, Euler’s insights - I’m not sure I’d be able to make much sense of them. I would certainly not be as proficient. This is not because the math was harder then than it is now, nor am I any less intelligent in this hypothetical, but because the mental framework, the cultural context, the interpretive tools I take for granted today simply didn’t exist yet.

It’s tempting, as students who learned about random sampling as preteens, to assume that intelligence is timeless - that any sufficiently clever student would have seen what Newton saw, could calculate a margin of error, or solved the Monty Hall problem on first glance. But that ignores how much of thinking is scaffolded by prior knowledge. We are all, to some extent, beneficiaries of the people who came before us - of the notations they invented, the mistakes they corrected, the consensus they reshaped.

So when I say I might have gotten the answer to the Monty Hall problem wrong, if I had no prior exposure, I don’t say it to be falsely modest. I say it to emphasize how hard-earned progress is - how even the “simple” truths we teach in classrooms often arrived only after years of confusion, debate, and resistance.

Science progresses in such a way that the most brilliant people in the world just a few decades ago didn't know or understand things that many high school students do today.

For some reason, in my experience, modern scientists do not appreciate this indisputable, humbling fact. They take past knowledge for granted as Something They Already Know, and forget how recently, and how painfully, these insights were earned. And that this lesson is one of the past, not the present or future. The result is a kind of intellectual hindsight bias: once a concept is absorbed into the collective knowledge base, it starts to feel like it was always there, like it didn’t take generations of struggle and error to uncover.

And this mentality produces sloppy thinkers who are unable or unwilling to innovate beyond their existing formulas, and understanding.

Isaac Newton once said:

“If I have seen further, it is by standing on the shoulders of giants.”

It’s a noble image: scientific knowledge accumulating steadily, each generation building on the last. But it's a myth.

The reality is, scientific knowledge does not accumulate steadily - it plateaus. It is flat and stagnant for long stretches, decades and centuries, bound by the assumptions and paradigms of the day. Scientists born on the shoulders of giants believe they have climbed there.

Then, seemingly out of nowhere, knowledge surges upward - propelled by a breakthrough that reframes the entire landscape. Often, this requires knocking off a few shoulder-sitters who don't believe in giving piggy-back rides themselves, and replacing them with climbers whose traps are more suitable for the job.

The history of science is not a gentle slope; it’s a staircase of upheavals. It is not giants standing on the shoulders of giants, it is David felling a giant, then calling more Davids to join him.

Mean Ol’ Marilyn

Marilyn vos Savant, a columnist for Parade Magazine, was posed the Monty Hall Problem in 1990 as part of her “Ask Marilyn” series.

Vos Savant, though rising to fame largely due to her record-reported IQ, was not a statistician or mathematician by trade. By all accounts, she does not even have a college degree.

Her answer to the Monty Hall Problem, however, was unequivocal:

1. Yes, it is advantageous to switch doors given the opportunity

2. Switching doors increases the player's win probability from 1/3 to 2/3

The backlash was instant and extreme.

Letters flooded in from math teachers, professors, and even PhDs and institutions like MIT - all insisting that her answer was wrong. She was accused of misunderstanding basic probability. They claimed she was misleading the public, and she should leave the math to the experts (and the men).

Some excerpts from critics:

“You blew it, and you blew it big!”

Scott Smith, Ph.D., University of Florida

“May I suggest that you obtain and refer to a standard textbook on probability before you try to answer a question of this type again?”

Charles Reid, Ph.D., University of Florida

“You are utterly incorrect… How many irate mathematicians are needed to get you to change your mind?”

E. Ray Bobo, Ph.D., Georgetown University

You made a mistake, but look at the positive side. If all those Ph.D.’s were wrong, the country would be in some very serious trouble.

Everett Harman, Ph.D. U.S. Army Research Institute

Maybe women look at math problems differently than men.

Don Edwards

MIT professors, who only much later realized Vos Savant was correct and they were wrong, seemed to think they were saving face by bragging about “computer models” to “check” the calculations she probably did in her head.

Of course, I refer to her as “Mean Ol’ Marilyn” not because she's mean - by all accounts she's exceedingly nice to people who know much less than her, even when they don't deserve it - but because it's gently ironic.

She became something of a folk villain to an entire generation of overconfident men with PhDs. They wrote her letters dripping with smugness, only to be politely - and devastatingly - corrected in public.

The Lessons Still Unlearned

To modern readers - especially students who’ve seen the problem in math class or online videos - it may seem absurd that anyone ever doubted this solution. But that very fact highlights something deeper: knowledge, especially probabilistic or counterintuitive knowledge, doesn’t just arrive fully formed in the minds of the many. It often begins in obscurity, and is validated only after resistance.

Years later, students and experts are taught the right answer, and the steps to solve it, and never have the opportunity to undergo the mental stress that comes with being forced to solve it themselves; many of my followers confidently declare that the solution is very easy. Perhaps it is, today, but just a few decades ago it clearly wasn’t. We are born on the shoulders of David Marilyn. Have some humility for the knowledge that you have - and understand that the only reason you think this problem is easy is because someone fought for it to be.

I think of this example a lot in existential terms: what do I truly know, if I can only know what I am taught? But to spare you, I'll continue.

The Monty Hall problem is, by any formal standard, elementary. It requires no calculus, no Bayesian inference, and no philosophical quandaries about consciousness or ethics. It can be solved on paper in its entirety in less than 10 minutes.

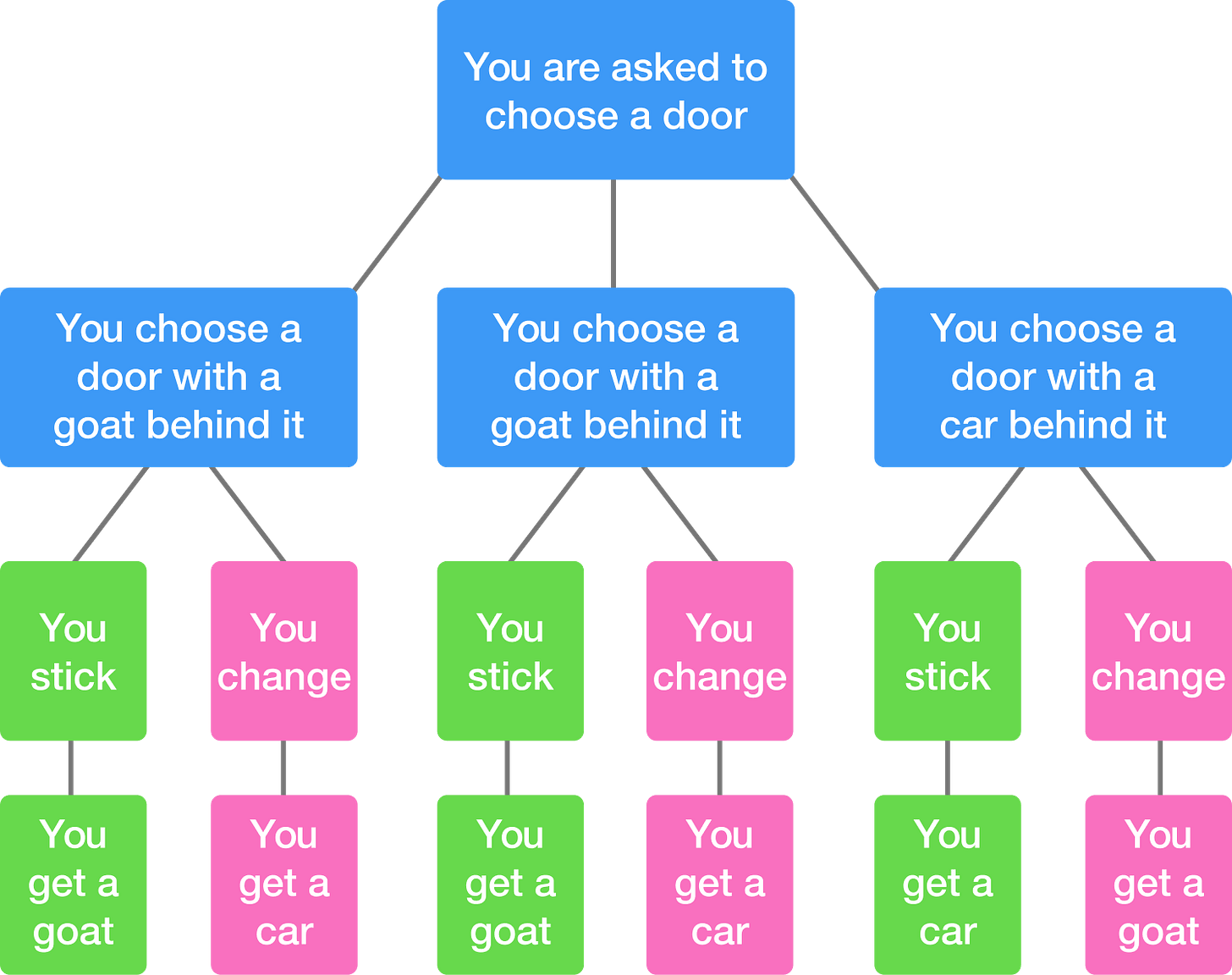
Vos Savant drew out a diagram similar to this to prove her solution. It is not complex.

It incorporates the three initial states, and all possible future states. It shows that initially there is a 1/3 chance, and switching yields a 2/3 chance. Computer models are great, but not exactly required.

And yet, not only did many of the most qualified people in the world get it wrong - but they refused to accept the answer even after it was proven. Not because of insufficient intellect - in most cases - but because of cognitive biases, a lack of probabilistic intuition, and perhaps most importantly, because the comfort of consensus had not yet shifted.

The most remarkable thing to me, reading the letters, is how many of them didn’t actually engage with Marilyn’s reasoning or math at all. They didn’t walk through the probabilities or point out a mistake in logic. Instead, they slung insults, flaunted their credentials, and appealed to some vague consensus - as if citing their PhD was a substitute for doing the math.

At a certain point, reading through the collection of letters published, I caught myself actually yelling; the content of that disappointment-driven anger is what caused me to draw some similarities to my work.

This is a math problem! No one gives a f**k what your name is or how many degrees you have, it literally does not matter. Here's the setup. Here's the analysis. Here's the conclusion. If I’m wrong, show me where, and show me how.

If you can’t, then shut the f**k up and get out of the way because you have nothing to contribute.

I'm not as nice as Marilyn, clearly. Though I suspect she fought her instincts as most of us would.

But when someone like Marilyn vos Savant calmly walks disagreeing experts through a problem they can’t solve, they don’t reconsider. They lash out. Because deep down, they’re not interested in the truth. They’re interested in people thinking they're right, and not being forced to admit they're wrong.

A New Consensus

The Monty Hall fiasco reveals a subtle but critical insight: the consensus doesn’t always track truth - it lags behind it. It lags behind it, and is often gatekept by unqualified practitioners.

Marilyn’s rapid exposure of this was only possible because of a nearly-impossible sequence of events:

1. She writes for a popular, national magazine

2. Someone asks a deceptively challenging statistical question

3. She is capable of solving it, solves it correctly, and the field's experts are loudly wrong contradicting her

These kinds of debates happen all the time in science. But they are usually among small cohorts, on issues most people don't care about, and are resolved (or not) mostly in private.

I don't think anyone could argue that if Marilyn vos Savant did not have a popular national magazine column, but nonetheless wrote to her local universities and organizations about how to solve the Monty Hall Problem (and how the consensus answer was wrong) it would probably have been ignored. She certainly wouldn't have received 10,000+ responses in the span of days.

And in the unlikely event of a response, would it have increased the agreement with her calculations among academics from 35% to 71% in just two years? How about increasing the public acceptance of her answer from 8% to 56% in the same timeframe?

Then it hit me like a ton of goats.

Consensus in science is not just scientific. It is social. It requires communication, persuasion, and (in the absence of a popular national column) something Max Planck may have known as “generational turnover.”

Even when the math is clear, ideas have to be absorbed into institutional knowledge, rewritten into textbooks, and taught by instructors who themselves might have initially opposed it. It's not enough to be right, relevant authorities have to be persuaded that you are, and humble enough to admit that they weren't.

The Monty Hall problem offers a case study in the importance of structured reasoning, and how otherwise smart people can be wrong.

Probability is notoriously resistant to intuition - humans evolved for survival, not probabilistic analysis and variable change.

But what’s more interesting is the lesson in epistemic humility: even when you are right, the world may not yet be ready to agree.

What I Care About

As my readers know, my research has led me to some remarkable conclusions about how Pre-Election Polls are poorly analyzed and understood, and my findings go as far as contradicting some foundational assumptions about the entire field of inferential statistics.

I am a scientist, not a networker or politician. I solve problems, I don't particularly care who likes me or not (despite the fact that I am probably quite likable in most settings).

I find the fact that an intelligent person would need to be “persuaded” about some objective fact detestable on its face.

What is true: The Election Result serves as a deceptive placeholder in the analysis of Pre-Election polls, leading to seemingly intuitive calculations like this one being both scientifically invalid and mathematically incorrect.

I have not just solved the problem, and illustrated in (I dare to say) elementary terms…

I have gone as far as explaining how to teach this to avoid reaching the wrong answer, inventing new terms to that end and even offering straightforward examples of where, how, and why existing calculations fail (but mine don't).

If you want to read about my findings, and how it will change science, here's a small selection:

How Polls Work and What Experts Get Wrong

Did Polls "Underestimate" Trump?

The Simultaneous Census Standard

Nate Silver should shut the f**k up about herding

The End of the Spread Method

Polls are not predictions

Silver & FiveThirtyEight: Wrong

The Snapshot Analogy (polls are blurry snapshots)

A Quick Poll Math Lesson

Them Don't Understand Polls

What the margin of error is (and isn't)

The Insanity of Assumptions (Step 1, Assume my Assumptions Can't Be Wrong) - one of the first things I wrote on here, it's pretty good.

If you want to read something I wrote even before political analysis, that illustrates the importance of understanding variable change: Stolen Bases and Variable Change

And of course, for brilliant people only:

The book