How poll "spreads" work

And why they're junk metrics

The most common metric cited in poll data is, by far, “spread” sometimes called “margin.”

The reason it is the most cited makes sense: it aims to simplify down to one number “who is ahead” and “by how much?”

It fails both tests.

Now, if this metric were used as a shorthand, approximate approximation, with the understanding that it is subject to many sources of error that have nothing to do with the poll - I could mostly forgive it.

But it's not.

It is used as the gold standard metric for FiveThirtyEight, and the AAPOR. This, from FiveThirtyEight:

They don't just believe the accuracy of polls can be ballparked using this method (which would be bad enough) they think it can be CALCULATED. This is junk science.

Every poll ever taken comes with a margin of error. The “spread” given by a poll throws it out.

Election results do not contain margins of error.

This metric compares one with a known margin of error to a result with none, and calls that the poll's error.

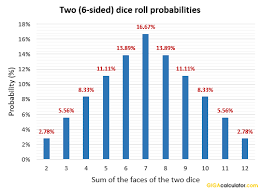
Let's talk dice

If you read stuff about poll data, you're probably not in need of basic probability lessons.

So here's a quick refresher on the odds of each sum rolling 2 standard dice:

If I were granted a 95% confidence interval, I would do pretty well to say:

Any given roll of two dice will produce 7 +/- 4.

That's a little off (it's something like 94.xx%) but for such an easy example, that gets us in the right space.

All good, right? A roll of two dice will produce a result of 7 +/- 4 with ~95% confidence.

Now,

1. Does my calculation say “7”? Did I say the next roll will be “7”? Spread calculators say it does. They say my calculation is wrong by the exact amount the next roll deviates from 7.

Spread calculations take a tool not designed to be predictive, a poll with a margin of error and confidence level, and judge it by how well it predicts a specific number. Junk.

2. Does my dice roll “poll” say that the dice roll will always be 7 +/- 4?

Of course not. Hence the whole “95% confidence” thing.

So here's bigger point number one:

Not only does it not say it will always be 7 +/- 4

It also says it will sometimes not be.

It doesn't say that “if things go wrong” or “if our calculations are not accurate” that the true value - in this case, the next roll - might be outside the margin of error.

It says that given enough rolls, you should expect that some are outside it!

They are inevitable, not failures. True, if my calculation produced results inside the margin of error only, say, 90% of the time that's a problem.

Bigger point number two:

If it produces results inside that margin of error far more frequently than you calculated (say, 99% of the time instead of 95%) that is also a red flag!

In poll discourse, it is popular to cite the largest outlier to defend the position that polls are/were inaccurate, but this mindset is just symptomatic of failing at probability.

Given a few hundred dice rolls, it is likely that some of them will produce “2s” or “12s”

Citing the twoest or twelvest poll of the hundreds of polls taken as evidence of their inaccuracy isn't saying anything other than you aren't good at math.

BIG SPREAD MEAN POLL BAD. Thanks for the expert analysis, G Elliott Morris.

2. Does my poll report of 7 +/- 4, say that the next roll will be 7?

When I put it this way, you get a glimpse of why spread is such a junk metric.

Remember, when analysts judge poll accuracy, they don't judge a poll according to whether or not it was inside the margin of error (a calculation they also don't understand) but by how close it was to “7.”

So let's put two equally qualified challengers against each other…and roll some dice.

In polls, even unrealistically assuming 0 undecided voters (which I'll build upon shortly) a poll that indicates both candidates are at “50%” doesn't know that for sure.

Equally, the next rolls for each candidate probably won't be exactly 7.

When I put it in terms of dice, it's obvious. But for some reason, when the subject changes to politics, people start acting stupid.

Every number given by a poll comes with a margin of error. No one who understands statistics would ignore it.

Assuming the poll had a 4% margin of error, what it says is:

Each candidate has 50% +/- 4% support, with 95% confidence.

A “50/50” poll could be 51-49 (with either candidate ahead) and even 53-47 with either candidate ahead…with no real error, other than the margin of error, which cannot be “fixed.”

With dice, we can calculate the probability of each outcome with certainty.

With polls, somewhat less so (though I'll be offering the definition of an ideal poll in something I'm working on currently).

Regardless, even if a poll were conducted perfectly by every possible measure, there's no way to eliminate the margin of error. Whether it's 2% or 4% or 20% all depends on the sample size. It can never be 0%.

Big point number three:

In poll data, fluctuation is normal and expected.

Assume, somehow, I knew with ABSOLUTE CERTAINTY that a given population had exactly equal support for two candidates: 50/50.

Taking a poll of this population, I'd expect my results to be…around 50/50. But like rolling exactly a 7, it's unlikely my poll produces exactly 50/50. Fluctuation is normal and expected.

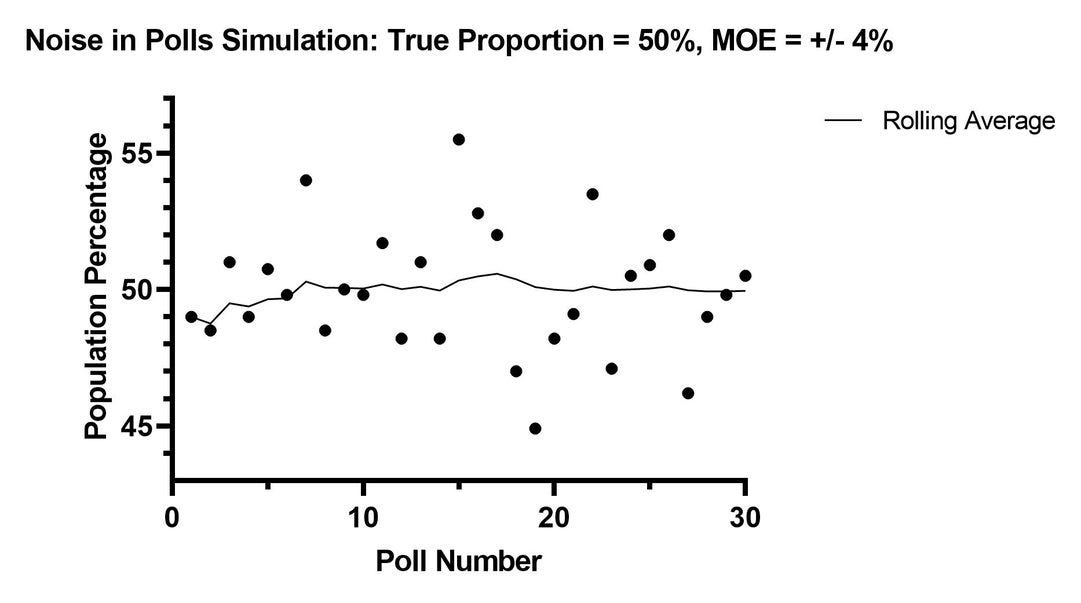
To illustrate, given a KNOWN population proportion of 50% (i.e. what is objectively true) a poll with a 4% margin of error would produce results ranging from 46%-54%, and only 95% of the time!

I illustrated in a simulation here:

That “spread” will range from 0-8 even for perfectly conducted polls - and that only represents results inside the margin of error - something a poll can't control!

Remember, each of those dots represents a poll taken perfectly from a population from a KNOWN proportion of 50%. So why do almost none say that?

Because that's how polls work.

This should be expected.

Now, let's talk about dice.

Specifically, two competitors rolling two different pairs of dice to see who wins, and by how much.

Want to predict the “spread”?

Both will roll a 7 +/- 4 with 95% confidence. We did the math.

So what should the spread be?

Now, this is fun.

Well, naturally, the spread “should” be around 0. Two people rolling two dice each, the odds of them rolling the same number are higher than any other possible outcome.

But should the spread be exactly zero?

And here’s why I could, kind of, forgive otherwise smart people for saying dumb shit like “difference in spread equals error” if they only used it as a very approximate, starting point, ballpark estimate:

“The spread should be kind of close” is a level of analysis might not get them an “A” in stats, but it won't fail them out either.

What does fail them:

“The difference in the rolls equals the error.”

Now we're getting into ignoring what the margin of error means.

If we took lots of polls about dice rolls, we would mostly get 7 +/- 4.

But the spread between single, competing rolls of two individuals has a very different look.

For example, if Candidate A rolls a 7, and Candidate B rolls a 6, then Candidate A wins by 1. That is plotted as “+1” below.

Since they are equally matched, the probability Candidate A LOSES by 1 is the same.

And so on for each possible outcome.

The largest possible spread is 10, because the largest number that can be rolled is 12, and the smallest is 2.

There are lots of highly possible outcomes (Candidate A rolls a 9, Candidate B rolls a 5, or vice versa) that would produce a seemingly large error, when in reality, there was no error. It was just chance.

When we talk about dice and simulations, people seem fine with fluctuation of performance, and everything being described probabilistically.

But when we talk about human actions, we have the false belief that what happened was the “correct” prediction. Why?

I suspect there are several contributing factors:

1. Hindsight bias

This is probably the largest. Elections are rare, and highly impactful events. What happened, in hindsight, feels like it should have been knowable.

2. Anthropocentrism

Not to get too philosophical, because human beings are far more complex than any science can (currently) quantify, but human actions - such as voting - have some amount of randomness to them.

If we could “go back in time” and the weeks leading up to each election were replayed 100s of times, the election results would be different every time. It might not be substantial, and the “winner” might not change often, but the results would never be exactly the same.

But if we were to retake each of the polls leading up to the election, not only would they be different every time, they could be substantially different. That's how polls work.

Human performance, while predictable in specific scenarios, can also be highly variable. The sports betting industry makes billions just by being good at human math. (Shameless plug)

Getting to +/- 4% with a 95% confidence level is really, really good.

But the “spread” is not what poll data tells us.

At its absolute best poll data tells us:

A current, approximate base of support for each option.

One individual with a poll number at “50” is not at 50. A single poll is definitionally incapable of providing data at that level of precision. It's much more likely it's not 50.

This is not to say we shouldn't judge polls by an objective standard (we can, if people in this field are interested in doing better math, use the simultaneous census standard) it's to say looking at individual polls, even the most recent poll, for some New Truth is - sorry - ignorant. See the “noise in polls” simulation again if you need to.

Read about the simultaneous census standard here.

Elections are not as simple as dice, but the probability of the range of outcomes is often as wide, sometimes wider.

Summarizing what a poll says by “spread” also ignores the second most valuable piece of data the poll can give: how many undecided voters.

A 49-49 poll (with 2% undecided) compared to a 45-45 poll (with 10% undecided) have the same spread.

But when there are more undecideds, the range of possible outcomes are much wider. If you're smart and interested in using polls to inform a prediction (because, unlike what experts will tell you, polls are not predictions) you should take this into account.

The probability one candidate wins by 5 is much higher with a 45-45 poll (or poll average) than a 49-49 one.

This should be obvious. But people who worship spread do not understand this simple fact.

Moreover, in elections with third-parties (which sometimes happen in the US, and often happen outside of it) these junk calculations demonstrate experts are incapable of quantifying the variables that matter.

A poll average that says 48-45 might be considered “close” (+3) but the candidate at 48 would be a consensus favorite.

But in an election with, say, 6% polled third party support (opposed to 7% undecided) the math isn't so easy. People who are polled as third-party supporters sometimes vote third-party - people who say they're undecided never vote “undecided.”

But there's more than that. A person who says they support the most conservative third-party candidate, if they do not eventually vote third party, is unlikely to vote for the more liberal major party one. Another simple calculation “spread” analysts are incapable of making - and why their “error” calculations often fail catastrophically.

The reason analysts shit the bed in the US in 2016 is because their junk metric is incapable of accounting for some major variables. When those variables are larger (third-party and undecided) that metric is more likely to fail.

Foreign elections, where third-parties and undecideds are often even higher (but the tradition is to lie and report polls with 0% undecided, and let the pollster guess what the undecideds will do) the math is even worse.

Spread, in polls, is a junk metric. It requires making poor assumptions and ignoring the margin of error. No one who understands polls would use it - and definitely not as any sort of standard.

Most of all, if you are using polls to inform some prediction about the future, spread is equally useless because it doesn't tell you:

1. How many third-party candidates there are, which impacts the finish line

2. How many undecideds there are, which impacts the variability/range of outcomes

I hate to be a nerd about it, but if you want to understand poll data, you might have to look at, like, at least 3 numbers (the two top candidates + undecided) to understand what it means, and not just one.

Sorry, experts.